Comparing Word Frequencies and Lexical Diversity with the ZipfExplorer Tool

Steven Coats
English Philology, University of Oulu, Finland, steven.coats@oulu.fi



5th DHN Conference
National Library of Latvia, October 2020

Outline

1. Visualization of frequency distributions

2. ZipfExplorer tool

3. Discourse comparison

4. Lexical diversity

Slides for the presentation are on my homepage at https://cc.oulu.fi/~scoats

Visualization of frequency distributions

If the word types in a text are ranked in decreasing order of their frequencies, the frequency $n$ of a word with rank $r$ is approximately inversely proportional to its rank (Zipf, 1935, 1949)

$$ n \propto r^{-z} $$

Where $z$ typically has a value close to $1$

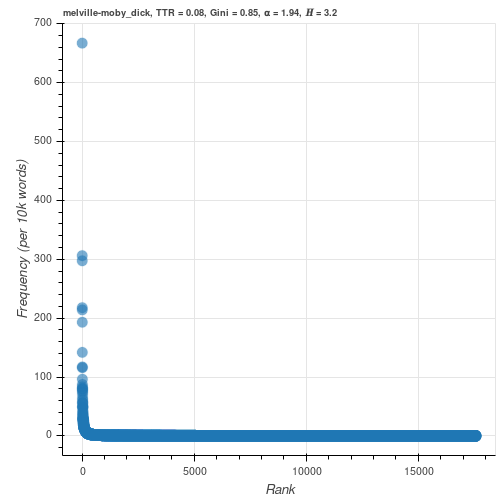
Taking the logarithm of both sides

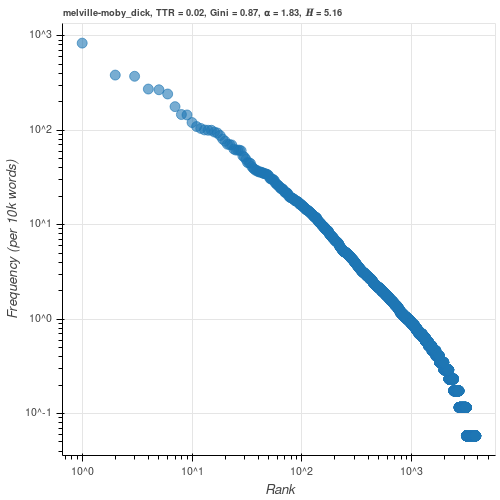
$$ \log{n} = -z \log r $$

yields Zipf's familiar rank-frequency plot when plotted in log-log space with slope $\approx -z$

ZipfExplorer tool

https://zipfexplorer.herokuapp.com

• Visualization of rank-frequency profile of shared vocabulary types in two texts (or one text)
• Individual word types can be selected and highlighted
• Frequent types can be removed
• Users can upload texts (in .txt format)
• Several lexical diversity measures calculated

• Created with the Bokeh package for visualization in Python (Bokeh Development Team, 2020)
• Advantage over (e.g.) Shiny, Plotly or Dash: Simultaneous interaction in two data frames
• Data: Texts from Gutenberg project, Brown and FROWN corpora, US presidential inaugural addresses (Francis & Kučera, 1979; Hundt et al. 1999; Bird et al., 2019)
• Github: https://github.com/stcoats/zipf_explorer

Discourse comparison

• Word types are presented in tables below the plots
• Types sortable by word, relative frequency, relative frequency difference, or log-likelihood score (Dunning, 1993; Rayson & Garside, 2000)
• Keywords (Stubbs, 2010) can shed light on discourse differences

Lexical diversity

• Type-token ratio
• $\alpha$ parameter of power-law distribution
• Gini coefficient
• Shannon entropy

Type-token ratio

$$ \frac{number~of~distinct~types}{number~of~tokens} $$

• Ranges from $\lim_{x \to 0^+}$ (no diversity) to $1$ (maximum diversity)

$\alpha$ parameter of power-law distribution

• Zipf's rank-frequency function is equivalent to the complementary cumulative distribution function of the Pareto distribution (Newman, 2005)

• If the frequency $n$ of a word with rank $r$ is $r^{-z}$, its derivative is a continuous approximation of the probability of encountering a type with frequency $n$

$$ f(n) \propto n^{-\alpha} $$

The new exponent $\alpha$ is related to the exponent of Zipf's Law:

$$ \alpha = 1+\frac{1}{z} $$

• if $z=1$, $\alpha=2$
• $\alpha$ is better-behaved as a random variable than is $z$ and is a better fit for actual texts (Moreno-Sánchez et al., 2016)
• The ZipfExplorer calculates $\alpha$ using the PowerLaw package (Alstott et al., 2014; Clauset et al., 2009)
• Typically ranges between $\sim1.5$ and $3$

Gini Coefficient

• Used to characterize wealth/income equality
• For $n$ word types with relative frequency $x$:

$$ \displaystyle G = \frac{2\strut\sum_{i=1}^{n} ix_i }{n\strut\sum_{i=1}^{n} x_i }-\frac{n+1}{n} $$

• Ranges from $0$ (equality) to $1$ (maximum inequality)

Shannon entropy

• The average amount of information, in bits, we need to represent a message (Shannon, 1948)
• For $n$ word types with relative frequency $x$:

$$H = -\sum\limits^{n}_{i=1}x_{i}\cdot log_{2}x_{i}$$

• High entropy: words not re-used

• Low entropy: words re-used

• Maximum entropy: $log_{2}n$

Summary

• Open-source tool for comparison of shared word frequencies
• Potential uses: Discourse analysis, distant reading, teaching (Zipf distributions, visualizations)

That's all! Thanks for listening!

References

Alstott, J., Bullmore, E. & Plenz, D. (2014). Powerlaw: a Python package for analysis of heavy-tailed distributions. PLoS ONE 9(1).

Bird, S., Loper, E. & Klein, E. (2019). Natural language processing with Python. Newton, MA: O'Reilly.

Bokeh Development Team. (2020). Bokeh: Python library for interactive visualization. http://www.bokeh.pydata.org, last accessed 01/03/2020.

Clauset, A., Shalizi, C. R. & Newman, M. E. J. (2009). Power-Law distributions in empirical data. SIAM Review 51(4), 661–703.

Dunning, T. (1993). Accurate methods for the statistics of surprise and coincidence. Computational Linguistics 19, 61–74.

Francis, W. N. & Kučera, H. (1979). A standard corpus of present-day edited American English, for use with digital computers. Providence, RI: Brown University.

Hundt, M., Sand, A. & Skandera, P. (1999). Manual of information to accompany The Freiburg – Brown Corpus of American English ('Frown'). Freiburg, Germany: Department of English, Albert-Ludwigs-Universität.

Moreno-Sánchez, Font-Clos, F. & Corral, Á. (2016). Large-scale analysis of Zipf's Law in English texts. PLoS ONE 11(1): e0147073. https://doi.org/10.1371/journal.pone.0147073

Newman, M. E. J. (2005). Power laws, Pareto distributions and Zipf's law. Contemporary Physics 46(5), 323–351.

Rayson, P. & Garside, R. (2000). Comparing corpora using frequency profiling. In: WCC '00 proceedings of the workshop on comparing corpora, pp. 1–6. New York: ACM.

Shannon, C. E. (1948). A mathematical theory of communication. Bell System Technical Journal 27, 379–423; 623–656.

Stubbs, M. (2010). Three concepts of keywords. In: Bondi, M., Scott, M. (eds.), Keyness in texts, pp. 21–42. Amsterdam: John Benjamins.

Zipf, George K. (1935). The psycho-biology of language. Cambrdige, MA: Riverside Press.

Zipf, G. K. (1949). Human behavior and the principle of least effort. Cambridge, MA: Addison-Wesley.